(1)SOLUZIONE DEI QUESITI PROPOSTI
ALLA PROVA SCRITTA DEL 27-09-2000
1) Studiare la convergenza puntale ed uniforme della serie:
(1)
La serie della somma è uguale alla somma della serie, quindi la serie 1 può essere studiata come somma di due serie:
Poniamo 
Il raggio di convergenza della serie è dato dall’inverso del limite:
=> r = 1
La serie converge puntualmente per –1<y<1 poiché
=> 
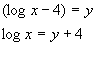e quindi 
per 
la serie diventa :
è la serie armonica che converge.
per 
la serie diventa 
convergente per Liebnietz.
Quindi la serie A converge uniformemente per 
per il criterio del confronto la serie Converge.
Quindi , in conclusione , la serie 1 converge uniformemente per